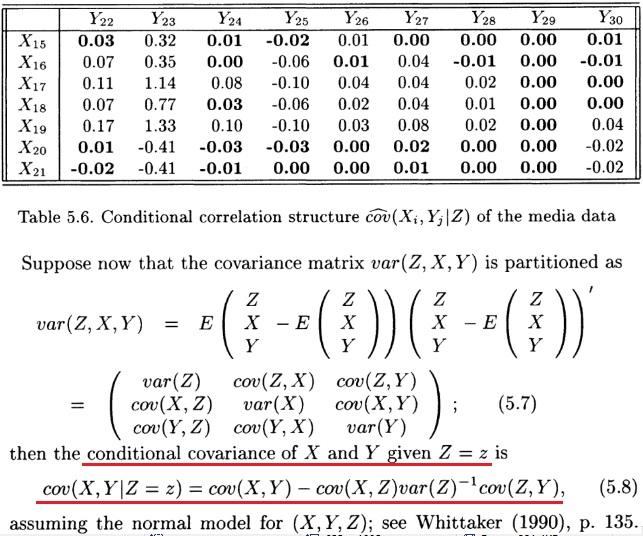
Instead of looking at the data as just intensity versus spectral channel, PCA attempts to construct a set of new vectors (also called features) that show as much variation in the spectra as possible. Imagine one has a dataset S which consists of N spectra with N spectral channels. The second principal component points in the direction of maximum variance that is not explained by the first principal component. The first principal component vector is parallel to the direction of maximum variance. These are called the principal components.
PCA works by producing a set of vectors that point along the direction of maximum variance while being simultaneously orthogonal to each other.
Principal component analysis (PCA) is a dimensionality reduction technique that attempts to recast a dataset in a manner that nds correlations in data that may not be evident in their native basis and creates a set of basis vectors in which the data has a low dimensional representation.